Коррекция эксцентриситета орбиты космического аппарата с магнитодинамической тросовой системой.

В последнее время необычайно возрос интерес специалистов к применению тросов в качестве элемента космических систем. Протяженные тросовые системы открывают новые возможности для операций в космосе, основанных на использовании статических, динамических и электрических свойств тросов. Научная и техническая мысль стремительно движется от первоначально фантастических проектов к совершенно реальным программам, полностью соответствующим современному уровню развития космической техники.

Орбитальные тросовые системы могут быть использованы для получения электрической энергии на борту и создания маршевой тяги. Эффекты, создаваемые ими, основаны на электромагнитных процессах, возникающих при взаимодействии токопроводящего троса с планетными и межпланетными магнитными полями и плазмой.

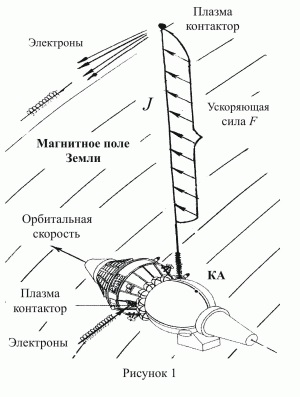
Электродинамическая тросовая система представляет собой космический аппарат (КА), снабженный вертикально гравитационно-градиентно-стабилизированным изолированным проводящим тросом, который заканчивается с обоих концов плазма-контакторами (рис.1). Плазма-контакторы – это устройства, обеспечивающие электрический контакт троса с плазменной средой Земли.

При движении тросовой системы в геомагнитном поле индуцируется электродвижущая сила, которая приводит к появлению разности потенциалов на концах троса. Для получения тока от этой разности потенциалов необходимо замкнуть электрическую цепь через трос, внешнюю плазму и ионосферу. В этом случае на прямолинейный трос будет действовать электромагнитная сила

где L - длина троса; J - вектор силы тока (направление вектора соответствует направлению течения положительного заряда); B - вектор индукции магнитного поля Земли. Для орбит, ниже геостационарной, эта сила будет иметь составляющую, тормозящую КА. Если же по тросу пустить заряд от бортовой энергетической установки против ЭДС индукции, то направление силы, действующей на трос, изменится на противоположное. Ее величина определяется также согласно (1), но только теперь F - ускоряющая сила.

Согласно предварительным оценкам, приведенным в /1/, при полете космического аппарата с электромагнитной тросовой системой на высоте 300…400 км в плоскости магнитного экватора при длине троса порядка 10 км и рабочем токе 10 А будет создаваться тяга примерно 2,5 Н. Изменяя направление этой тяги по определенным законам, можно корректировать все параметры орбиты КА (наклонение, большую полуось, эксцентриситет, долготу восходящего узла).

Исследуем возможность применения силы (1) для коррекции эксцентриситета орбит КА.. Предполагается, что в процессе полета трос остается прямолинейным и растянутым в направлении радиус-вектора КА. Центр масс системы считается совпадающим с центром масс базового КА. Компоненты вектора силы тока в орбитальной системе координат Oxyz представляются в виде:

где  - функция переключения направления силы тока; J - сила тока.

В первом приближении геомагнитное поле Земли можно представить полем магнитного диполя, ось которого наклонена к оси вращения Земли на угол /2/. Компоненты вектора индукции B в орбитальной системе координат определяются следующим образом /3/:

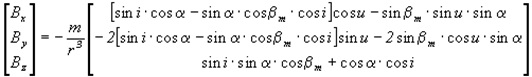
где i - наклонение орбиты КА;  - быстрая переменная, зависящая от времени t и угловой скорости вращения Земли; u - аргумент широты;  магнитный момент диполя; r - радиус орбиты КА.

Подставляя выражения (2) и (3) в (1) и определяя компоненты вектора силы, действующей на трос, можно заметить, что проекция силы на радиальное направление равна нулю, т. е.  Зная вектор силы, можно определить компоненты вектора ускорения. В безразмерной форме компоненты вектора ускорения имеют вид:

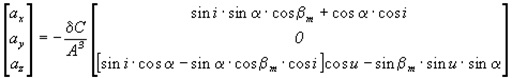
где - ускорение на начальной орбите;  безразмерный радиус орбиты;  ; R - - средний радиус Земли;  - начальная высота орбиты; - масса системы; μ - гравитационный параметр Земли.

Определим управление δ,  при котором происходит наибольшее изменение эксцентриситета. В принятых допущениях производная эксцентриситета по времени равна /4/:

где p - фокальный параметр орбиты; ν - угол истинной аномалии. 

Подставляя ускорения ax и ay согласно (4), получим:

Для того чтобы  производная эксцентриситета должна быть знакопостоянной функцией. Множитель всегда больше нуля. Выражение в скобках при условии  является положительной величиной при любом t. Таким образом, управление  приводит к росту эксцентриситета, а управление  к его уменьшению. Из формулы (5) также следует, что при постоянном управлении  δ=1 или δ=-1 производная эксцентриситета – знакопеременная функция, и общее изменение эксцентриситета за виток равно нулю.

Ниже представлены результаты численного моделирования движения КА с магнитодинамической тросовой системой. Моделирование проводилось в математическом пакете Maple 6. Начальные условия принимались следующие:

На рисунках 2 и 3 приведены графики зависимостей эксцентриситета и наклонения орбиты КА от времени для закона управления   и (для данных начальных условий неравенство  

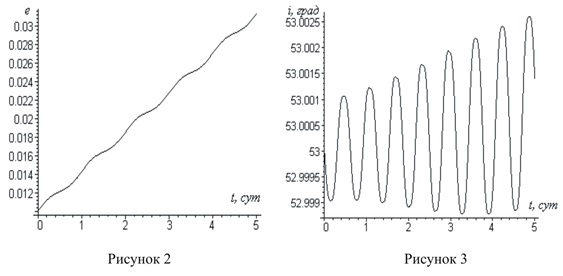
Как видно из приведенных графиков, при таком управлении эксцентриситет орбиты растет, а изменение наклонения незначительно. Как показывают расчеты, изменения всех остальных параметров орбиты КА, также как и наклонения, малы.

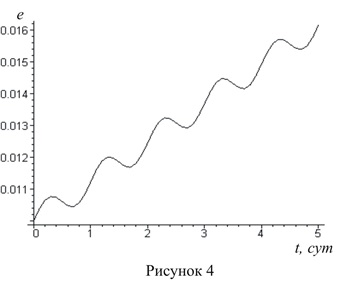
На рисунке 4 представлена зависимость эксцентриситета от времени для начального наклонения   В этом случае неравенство:  не выполняется, поэтому участки роста эксцентриситета чередуются с участками его уменьшения. В итоге, общее изменение эксцентриситета стало меньше. Для того, чтобы избежать этого, необходимо использовать более сложное управление, учитывающее знак выражения  Медленное изменение эксцентриситета при  обусловлено также тем, что при увеличении наклонения орбиты КА корректирующая сила (1) уменьшается вследствие уменьшения угла между векторами  B и J.

По результатам проведенных исследований можно сделать следующие выводы.

Сила, возникающая в результате взаимодействия проводника (троса) с током с геомагнитным полем Земли, может быть использована для коррекции наклонения, большой полуоси и эксцентриситета орбит космических аппаратов. Коррекция эксцентриситета возможна лишь при переменном управлении, знак которого изменяется при переходе через перигей и апогей орбиты  или  (если выполняется условие:  

). При изменении эксцентриситета все остальные параметры меняются незначительно. На скорость изменения эксцентриситета существенное влияние оказывает начальное наклонение орбиты КА.

Панина О.С.

Коррекция эксцентриситета орбиты космического аппарата с магнитодинамической тросовой системой

СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ

http://www.ssau.ru/resources/students/fla-2001/3/

1. Белецкий В.В., Левин Е.М. Динамика космических тросовых систем. М.: Наука, 1990. – 329 с.

2. ГОСТ 25645.126-85 Поле геомагнитное. Модель поля внутриземных источников. Введен в действие 01 января 1987 г.

3. Роберт Дж. Мак-Илвейн Изменение кинетического момента спутника при помощи магнитного поля Земли //Проблемы ориентации искусственных спутников Земли, М.: Наука, 1967.

4. Охоцимский Д.Е., Сихарулидзе Ю.Г. Основы механики космического полета.// М.: Наука, 1990. С. 242-248.