Correction of the eccentricity of the orbit of a spacecraft with a magnetodynamic rope system.
Recently, the interest of specialists in the use of cables as an element of space systems has increased unusually. Extended cable systems offer new opportunities for operations in space, based on the use of static, dynamic and electric properties of the rope. Scientific and technical thought is rapidly moving from the initially fantastic projects to absolutely real programs that fully correspond to the current level of development space technology.
Orbital cable systems can be used to generate electric power on board and create a thrust. The effects created by them are based on electromagnetic processes that arise during the interaction of a conductive cable with planetary and interplanetary magnetic fields and plasma.
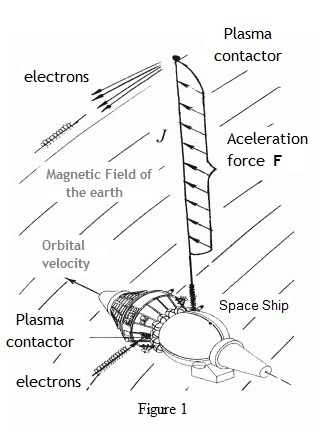
Electrodynamic tether system represents the spacecraft (SC) fitted vertically gravity-gradient-stabilized insulated conductive cable, which terminates at both ends of the plasma-contactor (Figure 1). Plasma-contactors - are devices that provide electrical contact with the cable Earth plasma environment.
When the rope system moves in the geomagnetic field, an electromotive force is induced these leads to the appearance of a potential difference at the ends of the cable. To obtain a current from this potential difference, it is necessary to close the electrical circuit through the cable, the outer plasma and the ionosphere. In this case, the electromagnetic wire will act on the straight cable
where L - length of the cable; J - the vector of the current (the direction of the vector corresponds to the direction of flow of the positive charge); B is the vector of induction of the Earth's magnetic field. For orbits below geostationary, this force will have a component that inhibits spacecraft. If you put the charge on-board power plant against the induced on the rope
The direction of the force exerted on the cable would be reversed. Its value is also determined according to (1), but now F accelerating force.
According to preliminary estimates, given in / 1 /, with the flight of the spacecraft with an electromagnetic rope system at 300 ... 400 km at the magnetic equator plane at cable length of 10 km and an operating current of 10 A is generated thrust approximately 2.5 h. By changing the direction of this thrust according to certain laws, it is possible to correct all parameters of the spacecraft's orbit (inclination, semi major axis, eccentricity, longitude of the ascending node).
We investigate the possibility of applying the force (1) for correcting the eccentricity of the orbit of spacecraft. It is assumed that during the flight the cable is straight and stretched in the direction of the radius vector of the spacecraft. The center of mass of the system is considered to coincide with the center of mass of the base spacecraft. The components in the current vector orbital coordinate system Oxyz represented as:
Where 
- function of switching the direction of current; J - the current.
In the first approximation, the geomagnetic field of the Earth can be represented by the magnetic dipole field, whose axis is inclined to the axis of rotation of the Earth by an angle / 2 /. The components of the vector of induction B in the orbital coordinate system defined as follows: / 3 /:
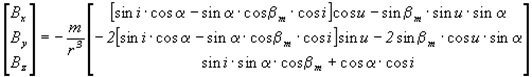
where i - inclination of the orbit of the spacecraft; 
- fast variable dependent on the time t and the angular velocity of rotation of the Earth; u - the argument of latitude; 
magnetic dipole moment; r - the radius of the satellite orbit.
Substituting expressions (2) and (3) in (1) and determining the components of the force vector acting on the cable, you can see that the projection of the force on the radial direction is zero, 
Knowing the force vector, we can determine the components of the acceleration vector. In the dimensionless form, the components of the acceleration vector have the form:
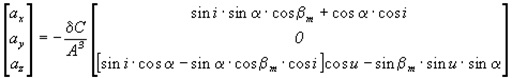
Where 
- - acceleration in the initial orbit; 
dimensionless radius of the orbit; 
; R - - the average radius of the Earth; 
- initial altitude of the orbit; - mass of the system; μ - the gravitational parameter of the Earth.
Define the control δ, at which the greatest change in eccentricity occurs. Under the assumed assumptions, the derivative of the eccentricity with respect to time is equal to / 4 /:
where p - focal orbit parameter; v - true anomaly angle.
Substituting acceleration a x and a y according to (4), we obtain:
In order to 
derivative of eccentricity should be sign-constant function. Factor 
is always greater than zero. Expression in brackets under the condition 
It is positive for any t. Thus, management 
leads to an increase in eccentricity, and management 
to its reduction. It also follows from (5) that under constant control δ = 1 or δ = -1 the eccentricity derivative is a sign-alternating function, and the total change in eccentricity per turn is zero.
Below are the results of numerical simulation of the motion of a spacecraft with a magnetodynamic rope system. Mathematical modeling was carried out in 6 Maple package. The initial conditions were as follows:
Figures 2 and 3 show graphs of eccentricity and orbital inclination KA versus time for the control law 
and 
(for these initial conditions the inequality 
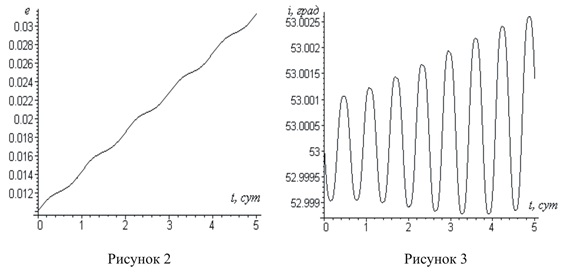
As can be seen from the above graphs, with such control the eccentricity of the orbit increases, and the change in inclination is insignificant. Calculations show that changes in all other parameters of the spacecraft's orbit, as well as inclinations, are small.
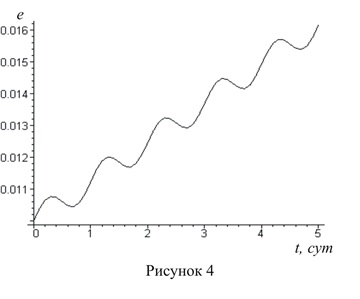
Figure 4 shows the dependence of eccentricity on time for the initial inclination
In this case, the inequality: 
is not fulfilled, therefore the areas of growth of eccentricity alternate with the areas of its decrease. As a result, the total change in eccentricity has become smaller. To avoid this, you must use a more sophisticated management that takes into account the sign of the expression 
slow change in eccentricity at is also due to the fact that as the inclination of the spacecraft's orbit increases, the corrective force (1) decreases due to a decrease in the angle between the vectors B and J.
Based on the results of the studies, the following conclusions can be drawn.
The force resulting from the interaction of the conductor (cable) with the current with the geomagnetic field of the Earth can be used to correct the inclination, the semi major axis and the eccentricity of the orbits of spacecraft. Correction of eccentricity is possible only with variable control, the sign of which changes when passing through the perigee and the apogee of the orbit or (if the following condition is satisfied:
).
When the eccentricity changes, all other parameters change insignificantly. The rate of change in the eccentricity is significantly influenced by the initial inclination of the spacecraft's orbit.
Panina O.S.
Correction of the eccentricity of the orbit of a spacecraft with a magnetodynamic rope system
LIST OF USED SOURCES
http://www.ssau.ru/resources/students/fla-2001/3/
- Beletsky VV, Levin EM Dynamics of space cable systems. Moscow: Nauka, 1990. - 329 p.
- The field is geomagnetic. Model intraterrestrial field sources. It was put into operation on January 1, 1987.
- Robert J.. Ilveyn Changing macro-kinetic moment of the satellite using the Earth's magnetic field // Problems orientation of artificial satellites, M .: Science, 1967.
- Okhotsimsky DE, Sikharulidze YG Fundamentals of the mechanics of space flight. // M .: Nauka, 1990. P. 242-248.